比特币代数曲线,揭秘加密货币背后的数学原理

比特币代数曲线：揭秘加密货币背后的数学原理

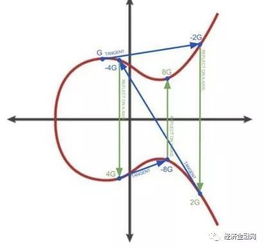
随着比特币等加密货币的兴起，越来越多的人开始关注其背后的技术。其中，代数曲线作为一种重要的数学工具，在比特币的加密体系中扮演着关键角色。本文将深入探讨比特币代数曲线的原理和应用。

一、什么是代数曲线

代数曲线是一种特殊的平面曲线，其方程为y^2 = x^3 + ax + b，其中a和b是常数。这种曲线在数学、物理和计算机科学等领域有着广泛的应用。在比特币中，代数曲线主要用于实现椭圆曲线密码学（ECC）。

二、椭圆曲线密码学

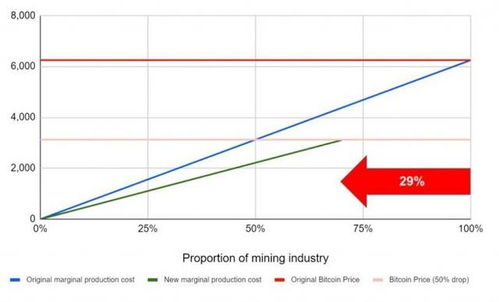
椭圆曲线密码学是一种基于椭圆曲线数学原理的密码学。它利用了椭圆曲线上的点加法运算，实现了高效的加密和解密过程。在比特币中，椭圆曲线密码学被用于生成公钥、私钥和数字签名。

三、比特币中的椭圆曲线

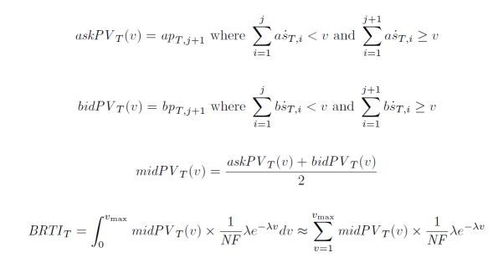
比特币使用的是一种特定的椭圆曲线，称为secp256k1。该曲线的方程为y^2 = x^3 + 7x + 65537，其中a=7，b=65537。secp256k1曲线具有以下特点：

有限域：椭圆曲线上的点构成一个有限域，其阶为n=2^256-977。

生成元：secp256k1曲线上的一个点G，其x坐标为0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798，y坐标为0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8。

私钥和公钥：在secp256k1曲线上，可以选择一个数字k作为私钥，并计算kG作为公钥。

四、比特币中的数字签名

数字签名是比特币中验证交易合法性的关键。在比特币中，数字签名是基于ECDSA（椭圆曲线数字签名算法）实现的。ECDSA签名生成过程如下：

生成私钥和公钥：在secp256k1曲线上选择一个数字k作为私钥，并计算kG作为公钥。

签名：对交易进行散列，然后使用私钥对散列值进行签名。

签名对的保存：将签名和公钥保存下来，以便后续验证。

五、比特币的安全性

比特币的安全性主要依赖于椭圆曲线密码学。由于椭圆曲线上的点加法运算具有以下特性：

不可逆性：给定两个点P和Q，无法直接从P+Q得到P或Q。

唯一性：对于给定的私钥k，其对应的公钥kG是唯一的。

因此，即使攻击者获得了公钥，也无法推导出私钥，从而保证了比特币的安全性。

比特币代数曲线作为一种重要的数学工具，在比特币的加密体系中发挥着关键作用。通过椭圆曲线密码学，比特币实现了高效的加密和解密过程，保证了交易的安全性和可靠性。随着比特币等加密货币的不断发展，代数曲线在加密领域的应用将越来越广泛。